力扣Hot100-图论篇
大约 6 分钟
200.岛屿数量
前置知识
网格图:
不同于普通图,网格图一般直接以二维数组的方式给出,例如该题:char[][] grid。
针对网格图,我们无需记录其边,对于每个结点其能移动的方向一般是固定的,例如上下左右(四连通)。
岛屿问题:
本题还是一道标准的岛屿问题,即网格图中每一个结点若是为 1,则代表一个陆地格子,相邻的陆地格子则构成岛屿;若是为 0,则代表海洋格子。
DFS 板子:
回想下,在二叉树问题中,是如何使用 DFS 的。
void traverse(TreeNode root) {
// 剪枝,不必再向下遍历了
if (root == null) {
return;
}
// 继续向下遍历,访问左右儿子
traverse(root.left);
traverse(root.right);
}
其中的两个关键点:
- 剪枝条件(二叉树中结点为空则进行剪枝)
- 向哪里访问(二叉树中是对左右儿子进行访问)
对应到岛屿问题:
- 剪枝条件(结点超出图的范围,结点为海洋格子,结点已遍历过,都需要进行剪枝)
- 向哪里访问(结点的上下左右四个方向的格子)
代码实现
class Solution {
private int dx[] = {0, 1, 0, -1};
private int dy[] = {1, 0, -1, 0};
private int n, m;
public int numIslands(char[][] grid) {
int count = 0;
n = grid.length;
m = grid[0].length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == '0' || grid[i][j] == '2') continue;
count++;
dfs(grid, i, j);
}
}
return count;
}
private void dfs(char[][] grid, int x, int y) {
// 结点超出图的范围,剪枝
if (x < 0 || x >= n || y < 0 || y >= m) return;
// 结点为海洋格子或已经遍历过,则也剪枝
if (grid[x][y] == '0' || grid[x][y] == '2') return;
// 遍历过的岛屿将其值设为 2
grid[x][y] = '2';
// 对当前结点的上下左右四个方向进行访问
for (int i = 0; i < 4; i++) {
int xx = x + dx[i], yy = y + dy[i];
dfs(grid, xx, yy);
}
}
}
994.腐烂的橘子
前置知识
BFS 中记录层数
本题要求返回:单元格中没有新鲜橘子为止所必须经过的最小分钟数。
要求遍历完整张图,且涉及到 最短/最小 这种字样,很容易让人想到 BFS。
而这道题也确实是使用 BFS 来完成,但有一个问题:
- 如何记录时间
解决方法:
- 在 BFS 中一次遍历一层,记录层数,也就对应腐烂橘子污染新鲜橘子所用的时间
代码实现
class Solution {
public int orangesRotting(int[][] grid) {
Queue<int[]> queue = new LinkedList<>();
int n = grid.length, m = grid[0].length;
// 记录新鲜橘子树
int count = 0;
// 1.将最初腐烂的橘子加入队列
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 2) queue.offer(new int[]{i, j});
if (grid[i][j] == 1) count++;
}
}
// 记录时间,亦是层数
int time = 0;
// 2.利用 bfs 进行遍历
while (!queue.isEmpty()) {
if (count == 0) break;
// 一次取出当前的一层
int size = queue.size();
time++;
for (int i = 0; i < size; i++) {
int[] org = queue.poll();
int x = org[0], y = org[1];
// 腐烂新鲜橘子,并将腐烂后的橘子加入队列
if (y + 1 < m && grid[x][y + 1] == 1) {
grid[x][y + 1] = 2;
queue.offer(new int[]{x, y + 1});
count--;
}
if (x + 1 < n && grid[x + 1][y] == 1) {
grid[x + 1][y] = 2;
queue.offer(new int[]{x + 1, y});
count--;
}
if (y - 1 >= 0 && grid[x][y - 1] == 1) {
grid[x][y - 1] = 2;
queue.offer(new int[]{x, y - 1});
count--;
}
if (x - 1 >= 0 && grid[x - 1][y] == 1) {
grid[x - 1][y] = 2;
queue.offer(new int[]{x - 1, y});
count--;
}
}
}
return count == 0 ? time : -1;
}
}
207.课程表
前置知识
拓扑序列
拓扑序列是对一个有向无环图而言的,有向图的拓扑序列是其顶点的线性排序,使得对每条有向边(u, v),u 在序列中出现在 v 之前,对于一个有向无环图而言,拓扑序列并不是唯一的。
举个例子吧: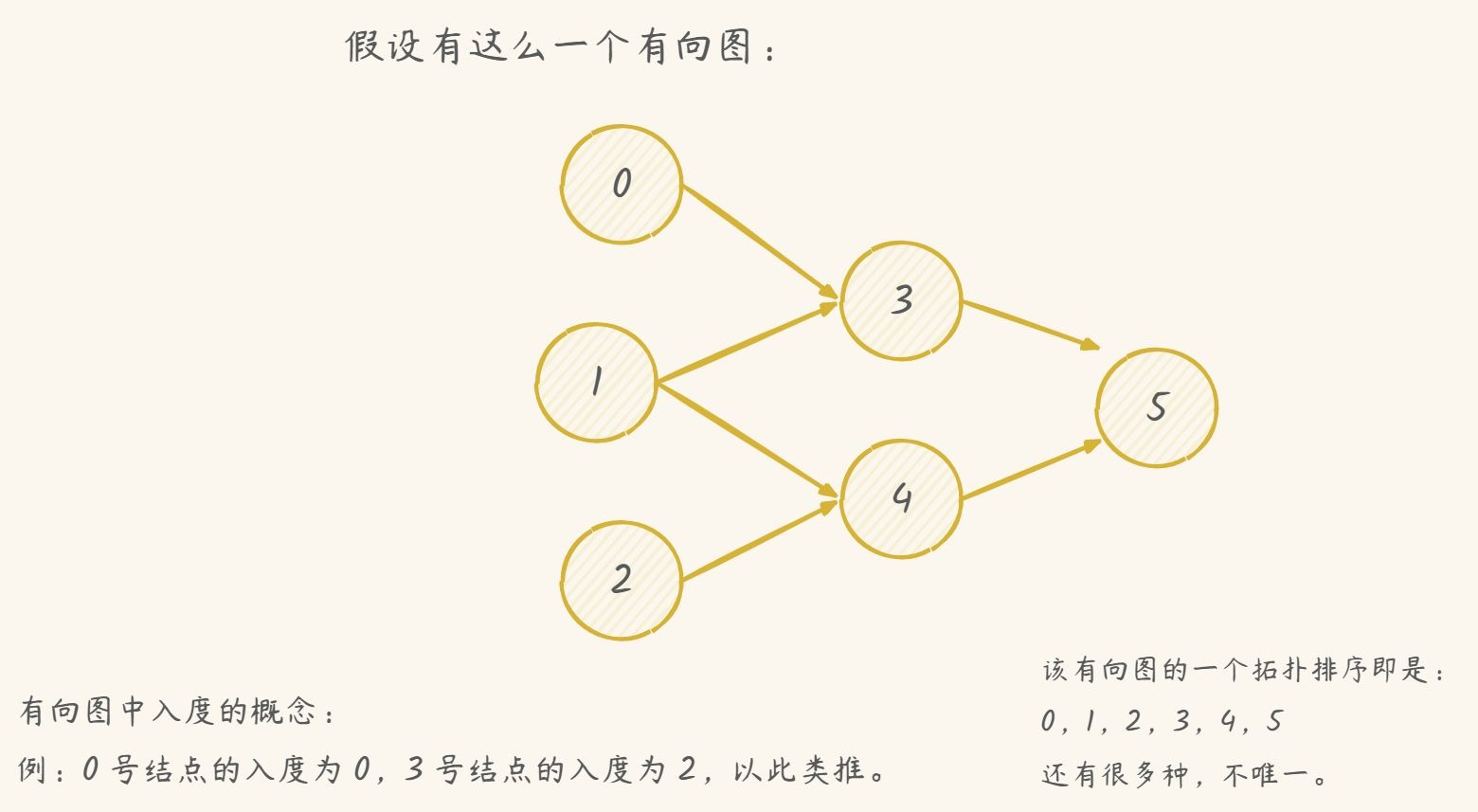
有了拓扑序列的前置知识,再回头看本题:
- 我们每次只能选当前能上的课,即入度为 0 的课,因为它不依赖其他课
- 选了入度为 0 的课后,依赖该课的课的入度要减 1,因为我们已经上了前置课程
- 以此类推,直至选不了入度为 0 的课
也就是说本题的本质就是让我们求图是否存在一个拓扑序列,如何求拓扑序列?通过 BFS,每次让入度为 0 的结点入队,以此来进行遍历。
代码实现
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
// 记录结点的入度
int[] inDegree = new int[numCourses];
// 记录映射,val 为依赖于 key 的课程集合
Map<Integer, List<Integer>> hashTable = new HashMap<>();
// 初始化
for (int i = 0; i < prerequisites.length; i++) {
int a = prerequisites[i][0], b = prerequisites[i][1];
if (hashTable.containsKey(b)) {
hashTable.get(b).add(a);
inDegree[a]++;
} else {
hashTable.put(b, new ArrayList<>(Arrays.asList(a)));
inDegree[a]++;
}
}
Queue<Integer> queue = new LinkedList<>();
// 将入度为 0 的结点入队
for (int i = 0; i < numCourses; i++) {
if (inDegree[i] == 0) {
queue.offer(i);
}
}
int count = numCourses;
// BFS
while (!queue.isEmpty()) {
int course = queue.poll();
count--;
if (count == 0) break;
List<Integer> list = hashTable.get(course);
if (list != null && list.size() > 0) {
for (Integer a : list) {
inDegree[a]--;
// 将入度为 0 的结点入队
if (inDegree[a] == 0) {
queue.offer(a);
}
}
}
}
return count == 0;
}
}
200.实现 Trie(前缀树)
前置知识
前缀树
先吐槽下,这道题真的能被划为图论么。。。
回想下,二叉树结点是怎么储存的:
public class TreeNode {
int val; // 当前结点值
TreeNode left; // 左孩子
TreeNode right; // 有孩子
}
那针对该题的前缀树结点又该如何储存呢?
class Trie {
private boolean isEnd; // 当前结点储存的值是否是一个完整单词的结束
private Trie[] next; // 字母映射,对于本题,next 的大小应为 26
}
关键点:
- 对于每一个前缀树结点,其孩子最多有 26 个,也有可能一个没有
- 每一个前缀树结点,我们并不知道其储存的值是多少,所以进行单词查找操作,都是从其孩子开始进行
代码实现
class Trie {
private boolean isEnd;
private Trie[] next;
public Trie() {
isEnd = false;
next = new Trie[26];
}
public void insert(String word) {
Trie node = this;
for (int i = 0; i < word.length(); i++) {
char ch = word.charAt(i);
if (node.next[ch - 'a'] == null) node.next[ch - 'a'] = new Trie();
node = node.next[ch - 'a'];
}
node.isEnd = true;
}
public boolean search(String word) {
Trie node = this;
for (int i = 0; i < word.length(); i++) {
char ch = word.charAt(i);
if (node.next[ch - 'a'] == null) return false;
node = node.next[ch - 'a'];
}
return node.isEnd == true;
}
public boolean startsWith(String prefix) {
Trie node = this;
for (int i = 0; i < prefix.length(); i++) {
char ch = prefix.charAt(i);
if (node.next[ch - 'a'] == null) return false;
node = node.next[ch - 'a'];
}
return true;
}
}
参考资料:
岛屿类问题的通用解法、DFS 遍历框架
「图解」拓扑排序 | 课程表问题
Trie Tree 的实现 (适合初学者)🌳
